Carbon footprint of the construction sector is projected to double by 2050 globally

Methodological overview

This study aims to specify whether the carbon emissions from the construction industry will preclude the Paris Agreement. Specifically, we quantify the magnitude of embodied carbon footprints in the global construction industry, identify specific contributions from supply chains, analyze the historical trend, develop future projections based on historical trends and socio-economic impacting variables, and compare with cumulative and per-annum carbon budget pathways for 1.5 °C and 2 °C goals. Input-Output Analysis^14,15,16,17 is first used to quantify the embodied carbon footprints from the global construction industry and identify specific contributions from supply chains (Methods, Supplementary Methods 1, Data S1). Following the carbon footprint estimation, we model future projections for global and specific regions based on panel OLS regression, fixed-effect regression^21,22, time-series forecast model, and simple linear extrapolation. We show that these regression results are congruent and robust. Last, we model the per-annum carbon budget trajectory for meeting the 1.5 °C and 2 °C Paris Agreement goals based on exponential decay function^26,27,28. We compare the forecasted cumulative and per-annum trajectories for the construction industry with the Remaining Carbon Budget (RCB) under the full range of possibilities (17%, 33%, 50%, 67%, and 83%). The following provides an overview of our methodological approach and further details discussed in Supplementary Methods 1-6.

Carbon footprints of the construction industry

The carbon footprints of the construction industry are calculated as the sum of the indirect and direct emissions.

where direct emissions are the emissions associated with on-site activities, and indirect emissions are the sum of emissions embodied in the full-supply chain, including the upper stream of services and materials related to the construction industry (see Supplementary Methods 1).

In terms of emissions estimation, the indirect emissions are calculated using the indirect carbon footprint intensity of each supply chain input. The construction industry’s footprint intensity is calculated through Input-Output Analysis (IOA)–a method that captures the full-supply chain footprints associated with an industry/region and is widely used in literature for footprint accounting^14,16,42,43. The calculation of footprint in IOA is established by solving a set of linear equations based on the input-output table. The set of linear equations is based on capturing the material and monetary transactions flow between industries and regions in the Input-Output table. Captured transactions include intermediate transactions, i.e., transactions of raw materials and semi-finished goods; final demand transactions, the ultimate destination of goods and services; primary input transactions, i.e., transactions of capital goods.

The 1995-2022 data from the global EXIOBASE input-output tables^18,20,44 are used to estimate the footprints of the construction industry. This is to reflect the full supply chain and transboundary emissions. The EXIOBASE input-output table contains 163 industries and 49 regions. The 49 regions include 44 countries (which cover 80% of the global GDP), and 5 Rest of World (RoW) regions, thus covering the scale of the entire global economy. This input-output table can reflect interlinkages of more than 100 million supply chains (see Supplementary Methods 1and Data S1) spanning across 163 industries and 49 global countries/regions.

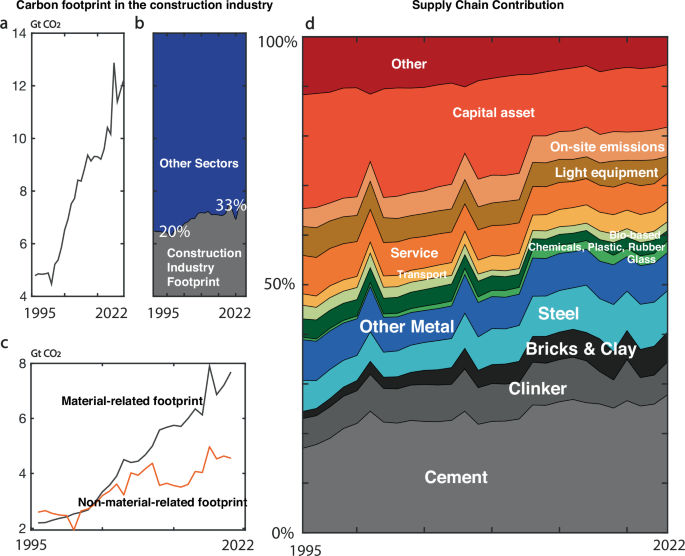
We first conduct screening and identification of the 163 industries to identify the supply chains that are most correlated with the construction industry. We do this through first calculating monetary and footprint interlinkages of individual supply chains on a global and regional level. From this step, we identify 13 supply chains that are most correlated with the construction industry: steel, cement, clinker, bricks and clay, biobased (including wood and fibers such as straws, see Supplementary Methods 1), glass, other metals, transport, services, light equipment, and capital assets. The rest of the industries combined are thus summarized under the “other” category (such as agriculture, food, apparels, etc.), given that their relevance to the construction industry is comparatively low.

We then calculate the full intensity matrix of the global economy, reflecting the supply chain interdependencies of construction-related carbon footprints (Eqs. 1–4). The calculation of embodied footprints builds on previous works by refs. ^16,43,45. Embodied footprints are then calculated by using the intensity matrix to map with monetary interactions indicated in IO tables (Eqs. 5, 6). The equation for solving the intensity of an industry is established as:

In Eq. (1), \({e}_{j}^{s}\) represents the resource/emissions from the environment (direct carbon emissions) into Industry \(j\) in Region \(s;{p}_{j}^{s}\) is the primary inputs into Industry \(j\) in Region \(s\); \({\varepsilon }_{p}\) is the embodied intensity of the primary inputs; \({t}_{{{\rm{ij}}}}^{{\mathrm{rs}}}\) is the intermediate inputs from Industry \(i\) in Region \(r\) into Industry \(j\) in Region \(s;{\varepsilon }_{i}^{r}\) is the embodied intensity of products manufactured by Industry \(i\) in Region \(r,{\varepsilon }_{j}^{s}\) is the embodied intensity of the products generated by Industry \(j\) in Region \(s;{x}_{j}^{s}\) is the industrial output of Industry \(j\) in Region \(s\), comprising \({\sum }_{r=1}^{m}{\sum }_{i=1}^{n}{z}_{{{\rm{ji}}}}^{{\mathrm{sr}}\,}\) (the amount of industrial output of Industry \(j\) in Region \(s\) that is used as intermediate inputs to all economic industries). By transforming Eq. (1) into matrix form could we obtain:

in which \(E={[{u}_{j}^{s}]}_{1\times {{\rm{mn}}}};\,P={[{p}_{j}^{s}]}_{1\times {{\rm{mn}}}}{;T}={[{t}_{{{\rm{ij}}}}^{{{\rm{rs}}}}]}_{{{\rm{mn}}}\times {{\rm{mn}}}};\,\varepsilon ={[{\varepsilon }_{i}^{r}]}_{1\times {{\rm{mn}}}}\); \({\varepsilon }_{p}={[{\varepsilon }_{p}]}_{1\times 1};\hat{X}\) is the diagonal matrix for \(X(={[{x}_{j}^{s}]}_{1\times {{\rm{mn}}}})\). It is worth noting that \({\varepsilon }_{p}\) is a scalar, which means that primary inputs into different economic industries are regarded to have the same embodied intensity; thus, we have \({\varepsilon }_{p}{\sum }_{s=1}^{m}\mathop{\sum }_{j=1}^{n}{p}_{j}^{s}=\mathop{\sum }_{s=1}^{m}\mathop{\sum }_{j=1}^{n}\mathop{\sum }_{r=1}^{m}{\varepsilon }_{j}^{s}{f}_{{{\rm{jO}}}}^{{\mathrm{sr}}}\), in which \({f}_{{{\rm{jO}}}}^{{\mathrm{sr}}}\) is the sectoral output of Sector \(j\) in Region \(s\) that is used as final demand^43,46.

Intensity is thus solved as

Embodied emissions of a supply chain is thus calculated as

where \({{{\rm{EES}}}}_{{{\rm{i}}}}^{s}\) stands for embodied emissions in supply chain \(i\) for region \(s\), \({\varepsilon }_{i}^{r}\) is intensity for input of materials from Region \(r\) Industry \(i\), and \({p}_{i}^{{rs}}\) stands for primary inputs from region \(r\) to region \(s\) in Industry \(i\). \({t}_{{{\rm{i}}}}^{{{\rm{rs}}}}\) is the intermediate inputs from Industry \(r\) to \(s\) in Region \(i\).

Embodied emissions of the direct onsite emissions for Region \(s\) is thus calculated as

where \({e}_{j}^{s}\) stands for direct emissions on the for region \(s\) industry \(j\).

The EXIOBASE provides information of direct emissions into each industry as satellite accounts. GHG emissions include carbon dioxide (CO2), methane (CH4), nitrous oxide (N2O), sulfur hexafluoride (SF6), hydrofluorocarbons (HFCs), perfluorocarbons (PFCs), and nitrogen trifluoride (NF3). We first estimate the full range of GHG emissions for the construction industry for single year and find that emissions from other GHG gases except CO₂ are minimal for the construction industry. Thus, here we only include CO₂ emissions (For further details please see Supplementary Methods 2).

Future projections

For future projections, we adopt a combination of four projection models: Time-series projection model, simple linear extrapolation, panel OLS regression, and fixed-effect regression.

Among the four types of projections, the time-series forecast and simple linear extrapolation for global footprints build on the observation that construction-related carbon footprints have followed a nearly linear trajectory with an almost constant growth rate over the past three decades (see Figs. 1, S1–2, Data S2). This makes it highly likely that future emissions will continue along a similar path. OLS and fixed effect regression are based on the reasoning that the evolution of construction footprint could be influenced by various socio-economic factors, such as GDP, population growth, urbanization, etc. We conduct these two types of regressions, each grounded in different underlying assumptions, independently for the global projections to minimize uncertainty. Results show that global projections remain highly robust across models. Regional projections carry greater uncertainty than global projections and are therefore treated separately (see Methods, Supplementary Methods 3).

Specifically, time-series forecast is based on the Autoregressive Integrated Moving Average (ARIMA) model²³—widely used in statistical analysis for time series forecasting. Linear extrapolation is based on the assumption of constant growth rate with historical evolution. OLS regression and panel OLS and fixed effect regression for multi-regional projections are then carried out. This is based on the reasoning that for countries projected to experience rapid increase of these socio-economic impact factors, the footprints from construction will be growing more rapidly. We test this hypothesis by analyzing the relationship between these variables both combined and in individual models by using historical data for three decades (Data S3). We found that these variables all have a statistically significant impact on construction carbon footprint, with population being the biggest impact variable (Data S3). This could be attributed to the fact that the construction industry is mainly supporting the housing needs and infrastructure for expanding population^3,47. To mitigate multicollinearity (as these socio-economic factors exhibit similar growth trends) and endogeneity (since other factors may also influence the construction footprint), we also utilize fixed-effect regression models^21,48. The socio-economic variables are based on Shared Socioeconomic Pathways database^25,49 (see Supplementary Methods 5). A combination of these regression techniques minimizes uncertainty (see Figs. S1–2).

To ensure robustness, a series of statistical tests is run prior to regression to avoid multicollinearity⁵⁰, autocorrelation⁵¹, heteroscedasticity⁵², etc. Tests such as KPSS (Kwiatkowski-Phillips-Schmidt-Shin), PP tests, Augmented Dickey-Fuller (ADF), Pearson Correlation Test, Ljung-Box Test, Durbin-Watson Test, ARCH and GARCH test are run. Below we provide an overview of the model settings; for details see Supplementary Methods 3-5.

Timeseries models for projection

We first define a baseline scenario where we assume the future trajectory of the construction industry remains the same growth speed in the last three decades. The baseline scenario is interpreted as a benchmark for understanding the projections for SSP projections, where socio-economic factors are also taken into account. The ARIMA model and linear model are used for this analysis. Our results show that the projections for linear extrapolation and ARIMA projections are most similar with the SSP2 (business-as-usual) scenario.

The ARIMA model is employed to forecast the future trajectory of construction-related CO₂ emissions based on historical data from 1995 to 2022. The observed time series of emissions is denoted as \({y}_{t}\), where t corresponds to the year. The model is defined as \({ARIMA}(p,d,q)\), where \(p\) represents the order of the autoregressive (AR) process, \(d\) is the degree of differencing applied to the data to ensure stationarity, and \(q\) is the order of the moving average (MA) process. Here we use a \({ARIMA}({\mathrm{1,1,1}})\) model, meaning that the model uses one lagged value of the time series to predict the current value \({y}_{t}\). This assumes that the immediate past influences the present in a linear fashion. We apply first-order differencing to the data to remove any trends, ensuring that the time series is stationary.

To fit the model, the algorithm estimates the parameters \(p\), \(d\), and \(q\) by minimizing the difference between the observed emissions and the values predicted by the model. The model fitting process is initiated by applying a first-order differencing to the data to account for non-stationarity, which results in \(\Delta {{{\rm{y}}}}_{{{\rm{t}}}}={y}_{t}-{y}_{t-1}\), thereby removing trends and stabilizing the mean of the series. The AR term of the model captures the relationship between the current value of emissions and its lagged values, such that

where \({{{\rm{\alpha }}}}_{{{\rm{p}}}}\) are the autoregressive coefficients. The MA term models the error as a function of past forecast errors, where the residuals are expressed as a weighted sum of past errors:

with \({{{\rm{\beta }}}}_{{{\rm{q}}}}\) as the moving average coefficients.

Once the model is fitted, the forecast for future values \({y}_{t+h}\), where \(h\) denotes the forecast horizon from 2023 to 2050, is generated using the ARIMA model. Forecasting is performed by recursively applying the AR and MA components to predict values for each subsequent year. The standard deviation of the residuals, denoted as σ, is then computed to provide a measure of uncertainty. Confidence intervals for the forecasts are calculated as \({y}_{t+h}\,\)± 1.96σ, representing a 95% confidence level.

Panel models for projection

To determine whether future construction industry can provide housing and infrastructure for population, we used OLS models to estimate relationships between historical population and construction carbon footprints for each individual country (Data S3). We base our projections of the construction industry by incorporating data from SSPs database. In our baseline estimations, we include regional and yearly fixed effects. The first accounts for unobserved, time-invariant differences between regions and the second accounts for unobserved, spatially invariant shocks that occur across all regions in a given year. These fixed effects help ensure that the estimated relationships reflect within-region, over-time variations rather than cross-regional or temporal shocks. By controlling for both, we mitigate the risk of omitted variable bias and focus on the specific dynamics of interest.

The regression model is set as

where \({{{\rm{\alpha }}}}_{1}\) captures the linear relationship between population and carbon footprint. The terms \({{{\rm{\alpha }}}}_{2}{{{\rm{\mu }}}}_{{{\rm{r}}}}\) and \({{{\rm{\alpha }}}}_{3}{{{\rm{\eta }}}}_{{{\rm{y}}}}\) are the region-specific and year-specific fixed effects, respectively. The error term \({{{\rm{\epsilon }}}}_{{{\rm{r}}},{{\rm{y}}}}\) represents the unobserved factors that may affect the carbon footprint but are not accounted for by population or fixed effects.

By incorporating region-specific fixed effects, \({{{\rm{\mu }}}}_{{{\rm{r}}}}\), we control for unobserved, time-invariant differences across regions such as structural economic factors, industrial composition, or institutional characteristics, which could affect baseline outcomes. By adding year-specific fixed effects, \({{{\rm{\eta }}}}_{{{\rm{y}}}}\), we control for time-varying, region-invariant shocks such as global economic cycles, technological advancements, or international policy changes. This approach helps ensure that the estimated relationship between population and carbon footprint is not biased by omitted variables. The projections for future construction activity are then informed by data from the Shared Socioeconomic Pathways (SSPs) database, which provides population projections under different future scenarios. These projections are integrated into the regression framework to estimate the potential future trajectory of the construction industry and its ability to meet housing and infrastructure demands.

Per-annum carbon budget modelling

In this study, we projected global carbon dioxide (CO₂) emissions pathways based on historical data and remaining carbon budgets (RCBs) aligned with the goals of limiting global temperature increase to 1.5 °C and 2 °C. The methodology employed involves the use of historical CO₂ emissions data and extrapolating future emissions trajectories based on the 2023 version of remaining carbon budgets.

The historical CO₂ emissions data from 1995 to 2022 were sourced from global emissions datasets and represent emissions in gigatons of CO₂ (GtCO₂) per year. To model the future pathways, we considered ten remaining carbon budget (RCB) scenarios, five each for 1.5 °C and 2 °C. For 1.5 °C, the RCB values are 500 GtCO₂, 300 GtCO₂, 250 GtCO₂, 150 GtCO₂, 100 GtCO₂^26,27,28. Each scenario corresponds to a probability of limiting the global temperature increase at 17%, 33%, 50%, 67%, and 83% possibilities, respectively. For 2 °C, the RCB values are 800 GtCO₂, 950 GtCO₂, 1150 GtCO₂, 1450 GtCO₂, and 2000 GtCO₂ at each corresponding to 17%, 33%, 50%, 67%, and 83% possibilities, respectively (seeSupplementary Methods 6, Fig. S3).

Following refs. ^26,27,28, projections were made using an exponential decay model. The decay in CO₂ emissions is driven by a decay constant \(k\), which is calculated separately for each carbon budget scenario. For each RCB scenario, the decay constant \(k\) was calculated using numerical integration to ensure that the cumulative emissions over the projection period matched the specified remaining budget.

To compute the correct decay rate for each scenario, we find the root which represents the decay constant \(k\) that ensures the cumulative emissions from 2022 to 2100 do not exceed the specified carbon budget under each scenario. The decay constant was determined by solving the following equation numerically:

where \({y}_{0}\) is the emissions in 2022 (41.5GtCO₂), \(k\) is the decay constant, and \(t\) is the year.

The modeled trajectory in our paper shows high consistency with projections from refs. ^26,27,28 For details of the trajectory figures and data see Figs. S1–3.